This research was developed in collaboration with Dr. Alba Perez-Gracia.
Overview
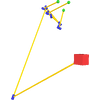
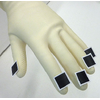
In this research we investigated the kinematic synthesis of tree articulated structures. In particular these structures are interesting as they are found in natural life forms. A straight-forward example would be the case of human hands that can be modelled using revolute joints. In order to be able to perform kinematic synthesis of these structures, we must understand the entire process in depth and establish criteria in which the system of equations does not degenerate. For this purpose we have presented both practical applications of this work and the more theoretical aspects of these structures.
We start by defining the system of equations needed to solve for tree topologies using Clifford algebra. An approach to solve the equations numerically using a hybrid optimizer based on Levenberg-Marquadt local optimizer and genetic algorithms was presented. We show that this approach is able to consistently find solutions despite the complexity of these equations that make them unsolvable by traditional methods.
We later extend this formulation to take into account velocities, accelerations and further derivatives using Lie algebra. We show that this simplifies the equation system and allows more control in the definition of tasks. By defining the proper velocity and derivatives at points in space it is possible to approximate arbitrary curves. Additionally the same optimization framework can be used.
Finally we do a more in-depth theoretical analysis of the conditions needed in order to be able to perform finite point kinematic synthesis on tree topologies. This is not as straight-forward as it seems as there may be sub-topologies that become overdetermined for certain tasks. This causes the equations to generate and not have any solutions. In order to avoid this problem, the topology must be analyzed in depth. We propose representing the topology as a compacted tree graph, and present the necessary criteria for the design equations to be solvable for a given task.
Full source code for all the publications is available.