測地混合モデル

There are many cases in which data is found to be distributed on a Riemannian manifold. In these cases, Euclidean metrics are not applicable and one needs to resort to geodesic distances consistent with the manifold geometry. For this purpose, we draw inspiration on a variant of the expectation-maximization algorithm, that uses a minimum message length criterion to automatically estimate the optimal number of components from multivariate data lying on an Euclidean space. In order to use this approach on Riemannian manifolds, we propose a formulation in which each component is defined on a different tangent space, thus avoiding the problems associated with the loss of accuracy produced when linearizing the manifold with a single tangent space. Our approach can be applied to any type of manifold for which it is possible to estimate its tangent space.

論文 ソフトウェア

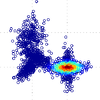
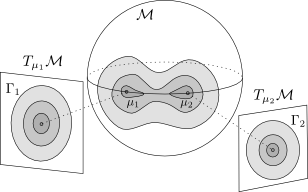
Overview of the Geodesic Finite Mixture Model By using multiple tangent spaces, one for each mixture, as shown on the left, we are able to minimize the approximation error of the linearization. As shown in the paper, using multiple tangent spaces allows much better accuracy in the estimation of the Probability Density function of the data in comparison to using a single tangent space or other manifold-specific distributions such as the von Mises-Fisher distributions for the sphere manifold.

We have released the code necessary for anyone to be able to reproduce the results in the paper. We have hopes that they will be useful and others will be able to find other manifolds in which the GFMM can be applied for interesting results.

Below we show the supplemental material provided with the paper. It is roughly a 2 minute video showing the expectation-maximization optimization process on two different synthetic scenarios presented in the paper.

論文

2016年

3D Human Pose Tracking Priors using Geodesic Mixture Models
3D Human Pose Tracking Priors using Geodesic Mixture Models
Edgar Simo-Serra, Carme Torras, Francesc Moreno-Noguer
International Journal of Computer Vision (IJCV) 122(2):388-408, 2016
PDF プロジェクトサイト ソフトウェア DOI
We present a novel approach for learning a finite mixture model on a Riemannian manifold in which Euclidean metrics are not applicable and one needs to resort to geodesic distances consistent with the manifold geometry. For this purpose, we draw inspiration on a variant of the expectation-maximization algorithm, that uses a minimum message length criterion to automatically estimate the optimal number of components from multivariate data lying on an Euclidean space. In order to use this approach on Riemannian manifolds, we propose a formulation in which each component is defined on a different tangent space, thus avoiding the problems associated with the loss of accuracy produced when linearizing the manifold with a single tangent space. Our approach can be applied to any type of manifold for which it is possible to estimate its tangent space. Additionally, we consider using shrinkage covariance estimation to improve the robustness of the method, especially when dealing with very sparsely distributed samples. We evaluate the approach on a number of situations, going from data clustering on manifolds to combining pose and kinematics of articulated bodies for 3D human pose tracking. In all cases, we demonstrate remarkable improvement compared to several chosen baselines. 
@Article{SimoSerraIJCV2016,
   author    = {Edgar Simo-Serra and Carme Torras and Francesc Moreno Noguer},
   title     = {{3D Human Pose Tracking Priors using Geodesic Mixture Models}},
   journal   = {International Journal of Computer Vision (IJCV)},
   volume    = {122},
   number    = {2},
   pages     = {388--408},
   year      = 2016,
}

2015年

Lie Algebra-Based Kinematic Prior for 3D Human Pose Tracking
Lie Algebra-Based Kinematic Prior for 3D Human Pose Tracking
Edgar Simo-Serra, Carme Torras, Francesc Moreno-Noguer
International Conference on Machine Vision Applications (MVA) [best paper], 2015
PDF プロジェクトサイト スライド ポスター DOI
We propose a novel kinematic prior for 3D human pose tracking that allows predicting the position in subsequent frames given the current position. We first define a Riemannian manifold that models the pose and extend it with its Lie algebra to also be able to represent the kinematics. We then learn a joint Gaussian mixture model of both the human pose and the kinematics on this manifold. Finally by conditioning the kinematics on the pose we are able to obtain a distribution of poses for subsequent frames that which can be used as a reliable prior in 3D human pose tracking. Our model scales well to large amounts of data and can be sampled at over 100,000 samples/second. We show it outperforms the widely used Gaussian diffusion model on the challenging Human3.6M dataset. 
@InProceedings{SimoSerraMVA2015,
   author    = {Edgar Simo-Serra and Carme Torras and Francesc Moreno-Noguer},
   title     = {{Lie Algebra-Based Kinematic Prior for 3D Human Pose Tracking}},
   booktitle = "International Conference on Machine Vision Applications (MVA)",
   year      = 2015,
}

2014年

Geodesic Finite Mixture Models
Geodesic Finite Mixture Models
Edgar Simo-Serra, Carme Torras, Francesc Moreno-Noguer
British Machine Vision Conference (BMVC), 2014
PDF プロジェクトサイト ソフトウェア ポスター DOI
We present a novel approach for learning a finite mixture model on a Riemannian manifold in which Euclidean metrics are not applicable and one needs to resort to geodesic distances consistent with the manifold geometry. For this purpose, we draw inspiration on a variant of the expectation-maximization algorithm, that uses a minimum message length criterion to automatically estimate the optimal number of components from multivariate data lying on an Euclidean space. In order to use this approach on Riemannian manifolds, we propose a formulation in which each component is defined on a different tangent space, thus avoiding the problems associated with the loss of accuracy produced when linearizing the manifold with a single tangent space. Our approach can be applied to any type of manifold for which it is possible to estimate its tangent space. In particular, we show results on synthetic examples of a sphere and a quadric surface and on a large and complex dataset of human poses, where the proposed model is used as a regression tool for hypothesizing the geometry of occluded parts of the body. 
@InProceedings{SimoSerraBMVC2014,
   author    = {Edgar Simo-Serra and Carme Torras and Francesc Moreno-Noguer},
   title     = {{Geodesic Finite Mixture Models}},
   booktitle = "Proceedings of the British Machine Vision Conference (BMVC)",
   year      = 2014,
}

ソフトウェア

GFMM
GFMM, 2.0 (2016年07月)
Geodesic Finite Mixture Models
詳細 github ダウンロード
This code is an implementation of the Geodesic Finite Mixture Models written in matlab. The core of the algorithm consists of a single file which can be called to perform the clustering. Additionally, several examples are provided to generate the figures from the paper.