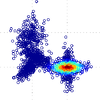
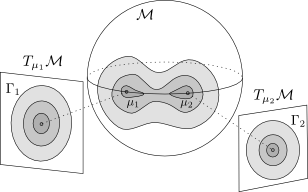
 By
using multiple tangent spaces, one for each mixture, as shown on the left, we are
able to minimize the approximation error of the linearization. As shown in the paper,
using multiple tangent spaces allows much better accuracy in the estimation of the
Probability Density function of the data in comparison to using a single tangent
space or other manifold-specific distributions such as the von Mises-Fisher
distributions for the sphere manifold.
By
using multiple tangent spaces, one for each mixture, as shown on the left, we are
able to minimize the approximation error of the linearization. As shown in the paper,
using multiple tangent spaces allows much better accuracy in the estimation of the
Probability Density function of the data in comparison to using a single tangent
space or other manifold-specific distributions such as the von Mises-Fisher
distributions for the sphere manifold.
We have released the code necessary for anyone to be able to reproduce the results in the paper. We have hopes that they will be useful and others will be able to find other manifolds in which the GFMM can be applied for interesting results.
Below we show the supplemental material provided with the paper. It is roughly a 2 minute video showing the expectation-maximization optimization process on two different synthetic scenarios presented in the paper.